周玉清,韩晓龙
(上海海事大学 物流科学与工程研究院,上海 201306)
集装箱港口是由岸桥,运输工具、场桥、堆场等组成的复杂系统。集装箱港口作业是由港口设备相互组合、相互协同完成的,这些设备的作业效率也直接影响了集装箱港口的作业效率。大型港口平均每天要处理几万TEU(Twenty-feet Equivalet Unit)的集装箱,因此港口设备之间相互协同作业的效率对于保证时间和成本效益非常重要,如何提高集装箱港口作业效率已成为当前集装箱港口研究重点关注的内容。目前我国集装箱港口主要采用的集装箱装卸船的工艺流程为船舶 → 岸边集装箱起重机→ 集卡→集装箱龙门起重机 →堆场。这种装卸工艺往往会出现设备之间相互等待的现象,造成设备之间的操作不协调,而集装箱跨运车(Straddle Carrier,SC)[1]可以从码头到堆场进行水平运输作业,也可以进行堆场的堆码、搬运和装卸作业,可跨越箱列,还可跨越铁路线路,实现一机多用,无需依靠起重机,减少运输设备与起重机的对齐抓取等作业环节、场桥等机械设备的使用等,可有效解决设备之间操作不协调的问题。当前跨运车技术在国外发展已到一定高度,国内无人跨运车技术正处于高速发展的阶段,因此研究跨运车在港口内的调度问题至关重要。
针对运输设备与岸桥之间协调问题,一些专家对提高岸桥使用率、优化改进岸桥作业模式以及运输设备作业模式进行研究,以提高港口作业效率:Goodchild 等[2]通过理论分析和数学演算证明了双循环岸桥的可行性,得出岸桥双循环操作可以减少10%的操作时间;
Zhang 等[3]考虑集装箱在船舶上的装载情况,优化岸桥最小作业循环次数;
常祎妹等[4]考虑装卸同步作业约束以及生产调度中的不确定因素,研究了不确定条件下的岸桥同步装卸问题;
孙清臣等[5]针对当前集装箱码头采用的双循环集卡操作策略,得出双循环操作策略平均能减少20%的装卸作业时间,并减少集卡空载率;
高熙等[6]设计了一种包含线性时间复杂度的岸桥最优调度构造算法,并证明了算法的高效性。
还有一些专家针对岸桥与水平运输设备等进行联合调度研究来解决港口设备不协调的问题:余孟齐等[7]考虑集装箱之间优先关系,研究了集装箱码头岸桥和集卡的集成调度问题;
Vahdani 等[8]整合了岸桥分配与内集卡共享,通过将内集卡分享到不同的码头岸线来实现码头工作量与内集卡之间的平衡;
梁承姬等[9]采用滚动窗策略研究岸桥集卡的联合调度问题,并用遗传算法进行求解,用以应对集装箱码头突发事件的发生;
Chen 等[10]采用三阶段算法研究岸桥与集卡的集成调度,采用启发式算法产生岸桥作业时间表,再进行集卡调度,最后得出完整的调度方案;
李坤等[11]关注了集卡与轨道吊的联系,以最小最大完工时间为目标,设计了两阶段禁忌算法求解;
马孙豫等[12]研究了双小车岸桥与自动导引小车(Automated Guided Vehicle,AGV)的协同调度问题,以AGV 调度为主,建立以卸船作业最末任务结束时间最小化为目标的模型,采用多层编码粒子群优化(Particle Swarm Optimization,PSO)算法进行求解;
张笑菊等[13]研究了岸桥同贝同步装卸时多环节作业协调问题,并设计启发式算法求解。
以上研究以岸桥与集卡为主要研究对象,都能有效提高码头作业效率,但当跨运车引入码头后,岸桥缓存区将大大影响码头作业效率。
在缓存区容量限制下,岸桥与跨运车之间的联合调度问题研究较少。汤鹏飞等[14]研究了在岸桥下方设置岸桥缓存区,对ALV(Autonomous Land Vehicle)行走路径进行优化;
Kress 等[15]构建了带缓存区单循环岸桥与跨运车的联合调度模型,并将弹射链加入禁忌搜索(Tabu Search,TS)方法中进行求解;
朱家栋[16]以跨运车到达码头前沿时间已知的背景下,将岸桥缓存区具体化为岸桥下车道,考虑了岸桥小车不能带箱跨越跨运车等实际情况,研究了岸桥与跨运车同步装船作业的优化问题,设计了双层遗传算法进行求解;
Chen等[17]建立跨运车双循环作业模型,利用禁忌搜索和模拟退火算法求解,发现在相同码头配置下,跨运车比AGV 作业效率更高;
安东等[18]研究了集装箱跨运车在中小型码头的应用模式,为跨运车进一步发展与应用提供理论基础;
Pellegrini 等[19]验证了在解决二次分配问题时,与禁忌搜索算法相比,响应性禁忌搜索算法稳定性更强。
现有的关于岸桥与跨运车的联合作业研究中,都在以岸桥或跨运车的固定作业序列下,研究另一方的作业序列优化,而未考虑岸桥与跨运车作业序列都不固定情况下,双方的联合作业问题;
且研究都是在岸桥单循环策略(岸桥先卸后装)或岸桥只卸只装下的研究,而岸桥双循环作业(岸桥可装可卸)与跨运车的双循环操作有更大的经济效益。因此本文将在岸桥与跨运车作业序列都不固定的情况下,研究双循环策略下岸桥与跨运车的联合作业序列优化问题来降低总体完工时间。
岸桥与跨运车的联合作业过程中,岸桥将船上的集装箱放在其对应的缓存区,直接由集装箱跨运车搬运和堆场堆码,两者互不干涉;
但当缓存区内箱位放满时,依然不可避免地出现等待时间。因此安排合理的岸桥与跨运车联合作业序列和缓存区容量,可有效解决以跨运车作为水平运输设备与岸桥进行联合装卸集装箱作业时产生的时空协调问题。
岸桥与跨运车在港口中的联合作业情况如图1 所示。对于出口箱作业,跨运车将集装箱从堆场运送至相应岸桥缓存区后离开进行下一个集装箱作业,岸桥将缓存区内集装箱进行装船作业;
对于进口箱作业,岸桥将集装箱从船舶上卸载放至其缓存区后进行下一个集装箱作业,跨运车将岸桥缓存区集装箱送至堆场相应位置。岸桥的双循环策略中,岸桥无需进行“先卸后装”作业,当岸桥将进口箱放置到缓存区后,若缓存区内有出口箱,可就近选择将出口箱放置船上,这样减少了岸桥空箱作业时间。跨运车双循环策略中,当跨运车将进口箱从岸桥缓存区运送到堆场中时,可选择不返回岸桥缓存区进行进口箱任务,而可就近选择进行出口箱任务,这样减少了跨运车空车返回的时间,可降低跨运车空载率。
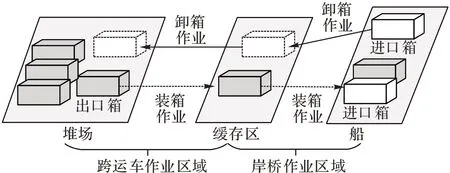
图1 岸桥与跨运车的联合作业流程Fig.1 Joint operation flow of quay crane and straddle carrier
本文以岸桥与跨运车为研究对象,针对双循环策略下岸桥与跨运车的联合作业序列优化问题,以总完工时间最小为目标,考虑岸桥缓存区容量限制、岸桥与跨运车联合操作、安全时间等约束,建立双循环策略下岸桥与跨运车联合作业的混合整数规划模型。然后设计基于贪婪算法的响应性禁忌搜索算法,得出最优的岸桥与跨运车联合装卸作业序列。最后,通过算例数值分析,讨论缓存区容量大小、跨运车数量,岸桥与跨运车配比对于岸桥与跨运车协同调度的影响。
2.1 模型假设
1)不同岸桥下方设置缓存区的容量大小保持一致;
2)跨运车一次作业一个集装箱,不考虑多载情况;
3)不考虑跨运车移动过程中的交通堵塞情况,不考虑翻箱问题;
4)岸桥装卸任意集装箱的时间相同、跨运车装卸任意集装箱时间相同,跨运车携箱与空箱移动速度相同。
2.2 符号说明
参数与变量如表1 所示。其中Rkj为人工变量,用来路径中保证不出现子回路,表示任务优先级,任务越靠后变量Rkj越大。

表1 参数符号说明Tab.1 Description of parameter symbols
集装箱进出缓存区时刻如表2 所示,规定集装箱离开与进入缓存区的时刻为岸桥或跨运车将集装箱在缓存区内提起或放下的时刻。

表2 缓存区内时间变量的描述Tab.2 Description of time variable in buffer
2.3 建立模型
本文主要目的是通过优化岸桥与跨运车联合作业序列,以降低全局完工时间,因此以最小化最大完工时间为目标,建立混合整数规划模型。
目标函数(3)表示,最小化最大完成任务时刻。对于出口箱,完成任务时刻为岸桥将集装箱放置在船上的时刻;
对于进口箱,完成任务时刻为跨运车将集装箱放置在堆场中的时刻。约束(4)(5)表示总完工时间为最晚结束任务的时刻。
M表示一个极大的数。约束(6)~(14)表示关于岸桥操作约束。约束(6)(7)表示同一个岸桥一次只能处理一个集装箱。约束(8)避免了每个岸桥的作业序列出现子回路。约束(9)(10)表示岸桥开始执行第一个任务的时刻,约束(9)表示如果岸桥第一任务为进口箱,则岸桥开始时刻大于等于0;
约束(10)表示如果岸桥第一任务为出口箱,则岸桥开始操作的时刻大于跨运车将集装箱放入缓存区的时刻以及安全时间之和。约束(11)表示岸桥处理两个任务之间的时间间隔大于岸桥在两个任务之间的空载移动时间。约束(12)表示岸桥结束处理任务i的时刻与开始处理任务i的时刻之差大于岸桥处理任务的时间。
约束(15)~(24)表示关于跨运车操作的约束。约束(15)(16)保证同一辆跨运车仅有一个后续任务和一个前序任务。约束(17)(18)表示在虚拟出发点派出的跨运车与返回虚拟结束点的跨运车的数量为一个定值。约束(19)表示跨运车不能从后续任务返回前序任务,不能直接从虚拟出发点到虚拟结束点,不能自循环。约束(20)(21)表示跨运车开始执行第一个任务的时刻,约束(20)表示每个跨运车负责的任务回路中,如果跨运车第一任务为出口箱,则跨运车开始时刻大于等于跨运车从初始位置到达任务点的时间;
约束(21)如果跨运车第一任务为进口箱,则跨运车开始时刻比岸桥将集装箱放入缓存区的时刻以及安全时间之和大。约束(22)表示跨运车处理两个任务之间的时间间隔比跨运车在两个任务之间的移动时间大。约束(23)表示跨运车结束处理任务i的时刻与开始处理任务i的时刻之差,大于跨运车处理任务的时间。
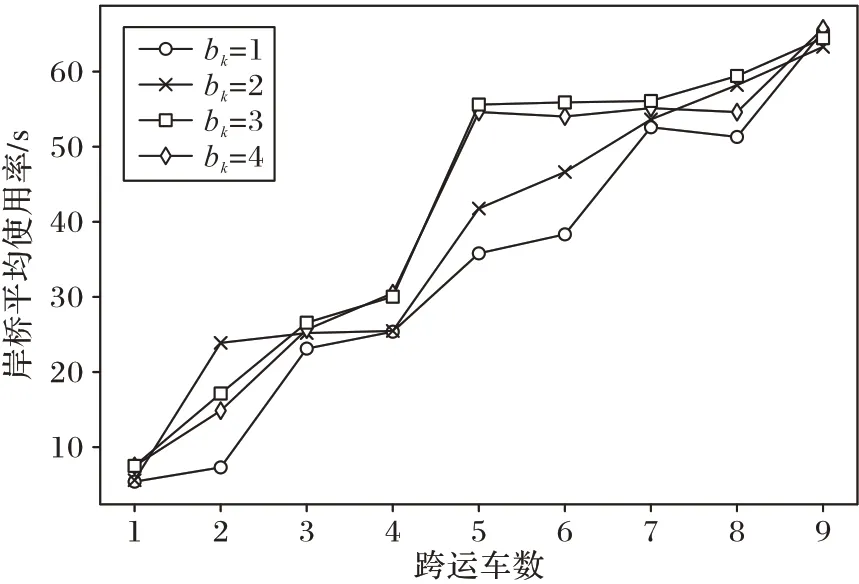
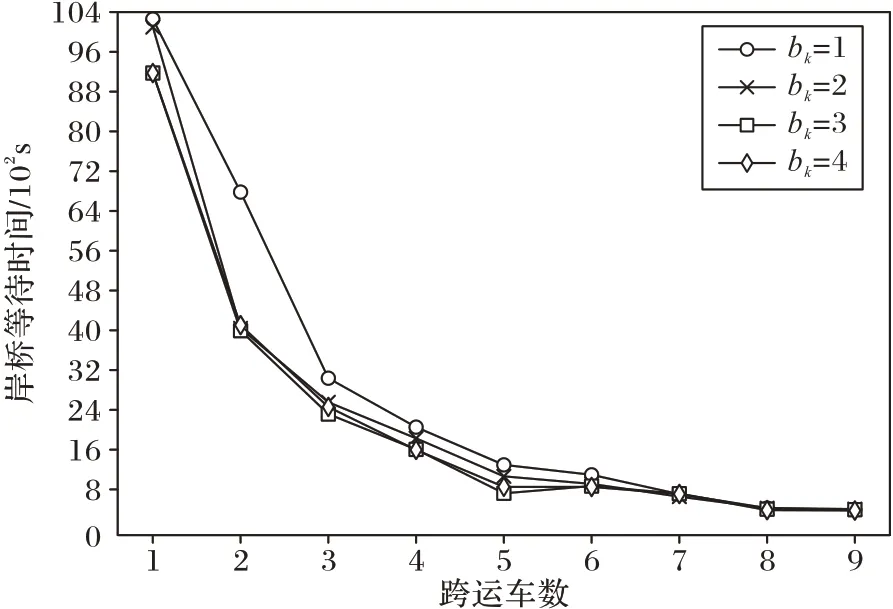
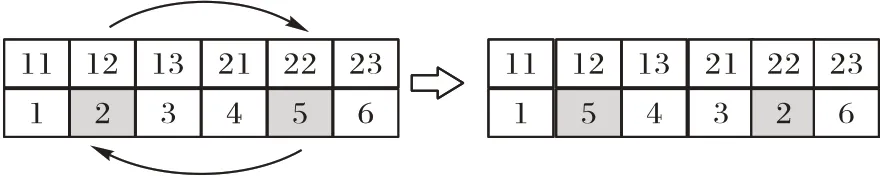
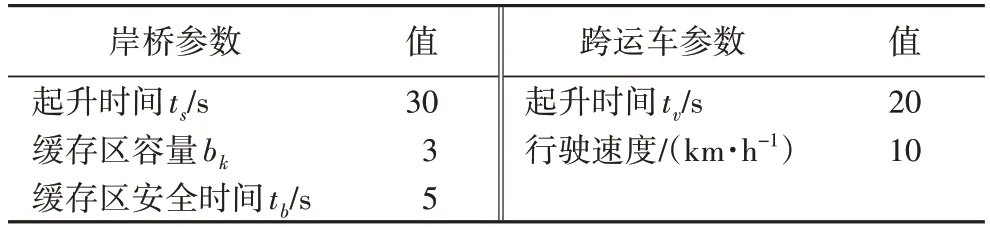
约束(25)~(36)表示关于缓存区的约束。约束(25)表示在k岸桥的j任务进入缓存区之前,缓存区中的集装箱数不超过缓存区容量。约束表示规定每个集装箱任务,必须在缓存区内停留tb的时间。约束(26)(27)表示安全时间约束; 本文所建模型的求解计算难度较大,属于NP 难问题。针对研究问题与模型特点,本文在求解岸桥和跨运车联合作业序列时容易出现死锁问题,因此在计算时会出现大量不可行解。而蚁群算法、遗传算法、模拟退火算法等属于概率性原理算法,应用于解决本文中问题时,局部搜索能力差,容易错失最优解。禁忌搜索(TS)算法可对局部进行大量搜索,更容易得到可行解,因此禁忌搜索算法较适合于本文的求解。 TS 算法是一种逐步寻优的邻域搜索算法,从初始解出发,标记已经解得的局部最优解或求解过程。然而传统TS算法对初始解的依赖性很强,且很难对某一特定问题确定有效的禁忌长度,难以避免搜索过早收敛,从而陷入局部最优,错失全局最优解。因此本文设计基于贪婪算法的响应性禁忌搜索算法用于求解模型,算法采用贪婪算法得到比较好的初始解,用多种邻域搜索策略将集中性搜索和多样性搜索策略相结合,保证邻域的多样性与集中性,且加入响应性禁忌搜索(Reactive Tabu Search,RTS)适时改变禁忌长度,加强TS 搜索机制,以求得全局最优解。 3.2.1 算法总流程 本文首先利用贪婪算法生成初始解,随后利用禁忌搜索算法改进初始解,从而搜寻出更好更优的解。算法流程如图2 所示。 图2 算法流程Fig.2 Algorithm flowchart 1)贪婪算法生成初始解流程。 步骤1 利用贪婪算法生成初始岸桥作业序列。 (a)将岸桥任务按照最早可开始时间从早到晚的顺序排列,得到集合Lk。 (b)集合Lk中的第一个运输任务作为第一台岸桥任务集合K1的第一个任务,即K1={li},计算该岸桥完成任务的工作时间T(K1)。将li从Lk删除。 (c)更新所有任务的最早开始时间,除li外所有进口箱开始时间推迟T(K1) +t,t为岸桥空箱返回船的时间,若出口箱最早开始时间小于T(K1),则出口箱最早开始时间更新为T(K1),否则不变。 (d)若Lk≠∅,返回步骤1(a),否则,进入步骤1(e)。 (e)岸桥k的作业任务分配完成,任务集合为K1。开始为下一个岸桥分配任务,直到所有岸桥任务分配完成。 步骤2 根据岸桥作业序列,忽略跨运车分配问题以及缓存区容量问题,仅考虑集装箱从起点到达终点的运输时间,生成集装箱最早作业时间表以及最晚作业时间表。 步骤3 确定跨运车运输序列。根据集装箱作业时间表,按照集装箱作业时间表中的优先关系,运用贪婪算法为多辆跨运车分配运输任务。 (a)将跨运车作业任务按最晚开始时间从早到晚的顺序排序,排序集合为L。 (b)集合L中的第一个运输任务lki(k∈K,i∈J)作为第一辆车辆任务集合V1的第一个任务,即V1={lki},并计算该车辆完成该任务的工作时间T(V1),此时第一辆车辆为距离任务lki出发地最近的车辆,从L中删除lki。 (c)从集合L中寻找出发地与任务lki目的地的距离较近的任务集合,并从中寻找最晚出发时刻小于或等于完成任务lki时刻的任务。分别计算完成该任务的时刻,取完成任务时刻最小的任务lkj作为该车辆的第二个任务,并将该任务加入V1,更新T(V1),从L中删除lkj。 (d)根据步骤3(c)依次为第一辆车辆分配任务,当所有任务的最晚出发时刻小于T(V1)时,第一辆车辆的运输任务分配完成,任务集合为V1。开始为第二位车辆分配任务。 (e)依次按照步骤3(b)~(d),依次为所有车辆分配任务,直到所有车辆以及所有任务分配完成。 步骤4 初始值生成。根据所生成的岸桥与跨运车的作业序列,考虑缓存区容量,调整岸桥与跨运车的实际作业时刻表,并计算岸桥与跨运车完成任务的最大时刻W。 2)改进解流程。 步骤5 初始化。W作为初始值,将此时的岸桥作业序列以及跨运车作业序列作为初始解S。 步骤6 输入算法参数:最大迭代次数rmax、最大候选集数目nmax、候选集N、禁忌表1(Tabu1)、禁忌长度(T1)、禁忌表2(Tabu2)和禁忌长度(T2)。 步骤7 根据Tabu1、T1,利用交换、逆序等方式产生候选序列,作为岸桥作业序列,将此序列加入Tabu1。 步骤8 根据岸桥作业序列,利用贪婪算法生成跨运车作业序列。根据Tabu2、T2,利用交换、逆序等方式产生候选序列,作为跨运车作业序列,将该候选解加入候选集N,n=n+1,若n 步骤9 对N中的候选解进行解码计算,选出当前最优解S",记录其适应度值W(S")。 步骤10 更新当前最优解,更新Tabu2,将W(S")代入RTS 策略(见4.3.3 节RTS 算法),动态调整T2。 步骤11 禁忌搜索算法迭代终止检验。检验是否达到最大迭代次数:若是,则进入步骤13; 步骤12 更新Tabu1,将W(S")代入RTS 算法(见4.2.4节RTS 算法),动态调整T1,进入步骤7。 步骤13 输出全局最优解。 3.2.2 编码方式 编码方式如表3 所示。表3 中任务的编号11 表示第1 台岸桥的第1 个任务。第二列表示每个岸桥处理任务的优先级,数字越小优先级越高,例如第1 个岸桥任务序列为11-12-13-14-15,第二个岸桥的任务序列为23-22-24-21-25。第三列表示跨运车处理任务的优先级序列; 表3 编码表Tab.3 Coding table 3.2.3 邻域结构设计 禁忌搜索算法邻域设置。禁忌搜索基于邻域变换进行搜索,确定邻域操作至关重要。本文选用3 种应用于车辆路径问题的邻域结构,操作时随机选择其中一种。例如跨运车任务优先级序列为φ={1,2,3,4,5,6},阴影处为随机选择的两个任务i和j。 1)Exchange:随机选择任务i和j的位置互换,得到:1-4-3-2-5-6,则跨运车序列为11-21-13-12-22-23。 图3 ExchangeFig.3 Exchange 2)2-Opt:随机选择任务i和j之间的任务逆序,得到:1-5-4-3-2-6。 图4 2-OptFig.4 2-Opt 3)Glover 等[20]提出了一个多样性搜索策略的方法程序,通过定义步长对置换重新排序,从当前全局最优解创建新解。从步长(step)2 开始,每次重新启动算法时,步长都会增加,必要时循环回到原始步长。 多样性搜索策略程序步骤。 步骤1 初始化。 1.1)令当前全局最优解为初始解S; 1.2)令k=1,start=step,j=start,η为一个空集。 步骤2 生成邻域解。 2.1)将元素j加入集合η中,令S(k)=ϕ(j); 2.2)令k=k+1; 2.3)若j 2.4)若start>1,则start=start-1,j=start,否则结束。 2.5)如果j∉η,则进入步骤2.1); 为说明上述方法,考虑以下置换示例。 原解为:φ={1,2,3,4,5,6}。 选择步长step=2,算法初始化的第一次迭代将初始变量j转换为2,在本例中,该迭代导致j的变化范围为公差为2的等差数列,则S中的元素逐个被φ(j)取代。在本例中n=6。在start=2 时的第一次迭代之后,得到以下部分置换:S={2,4,6,_,_,_}。 最后,通过步骤2(d)的传递将start设置为1,并获得以下完整排列S={2,4,6,1,3,5}。以这种方式,对于每个步长,获得不同的排列,以扩大邻域搜索范围。 3.2.4 禁忌对象与禁忌长度 禁忌对象为任务序列。针对3 个不同的邻域搜索方法设置3 个不同的禁忌表。禁忌长度为每个禁忌对象在禁忌表中的储存时间。禁忌长度过短,可能进入循环无法跳出; RTS 算法具体步骤如下: 步骤1 初始化RTS 相关参数。 步骤2 RTS 算法框架。 2.1)生成候选解,找出当前最优解。 2.2)把当前最优解存入Hash 表,判断是否重复:若重复,转步骤2.3); 2.3)解重复次数repeat=repeat+1,若repeat>remax,转步骤3; 2.4)判断重复间隔regap,若regap>gapmax,禁忌长度T=T×increase; 2.5)判断当前时间距离上次禁忌长度发生改变的时间是否超过预设值,若超过,则T=T×decrease,转步骤4。 步骤3 逃离机制。跳出当前搜索区域,利用多样性搜索策略,即策略3(见3.2.3 节3))重新生成初始解进行搜索。 步骤4 算法终止。达到预先设定最大迭代步数,算法终止。 算例中设备参数来源于文献[5,15,21]。设置3 个岸桥,4 个跨运车,每个岸桥有5 个需要装卸的集装箱,共15 个任务。表4 为参数,表5 为任务集合。 表4 参数Tab.4 Parameter 表5 任务集合Tab.5 Task collection 利用基于贪婪算法的响应性禁忌搜索算法对该算例进行求解,算法收敛情况如图5 所示。最终得到的目标函数值为2 345 s,任务序列如表6 所示。在该算例下岸桥与跨运车的联合作业序列:岸桥1 为12-15-14-11-13,岸桥2 为22-24-23-21-25,岸桥3 为34-33-32-31-35; 图5 基于贪婪算法的响应性禁忌搜索算法收敛图Fig.5 Convergence graph of responsive tabu search algorithm based on greedy algorithm 表6 联合作业任务序列Tab.6 Joint operation task sequence 表7 岸桥与跨运车调度表Tab.7 Scheduling table of quay crane and straddle carrier 通过表7 可以看出在岸桥与跨运车双循环操作策略下,岸桥无需直接开始装卸作业,具有一定的缓冲时间,这是由于跨运车到达缓存区需要一定的时间,或在调度安排下,跨运车从堆场运输出口箱至缓存区需要一定的运输时间。 为验证本文算法有效性,参考文献[16]设计算例,将本文算法与CPLEX、传统禁忌搜索算法、遗传算法求解结果进行分析比较,结果如表8 所示。 从表8 中,可以看出当任务量较少时,CPLEX 计算速度较快,两者计算目标值相等,而当任务量达到15 时,CPLEX计算时间大于90 min,而本文算法计算时间为26 s,且计算结果无偏差。 表8 算法性能分析表Tab.8 Algorithm performance analysis table 与传统禁忌搜索算法相比,本文算法在求解速度上具有明显优势,且求解效果更好,而当任务规模达到45 时,传统算法很难搜索出可行解。因此基于贪婪算法的响应性禁忌搜索算法可很好地解决跨运车与岸桥的调度问题; 本节将重点分析缓存区容量与跨运车的数量、岸桥与跨运车数配比对总体作业时间快慢的影响。为评估缓存区容量的设置以及跨运车数对整个调度过程产生的影响,利用上述算例数据设置两组实验。 实验1 缓存区与跨运车影响分析。 实验1 设置集装箱量为15,其中出口箱量为8,进口箱量为7。岸桥数为3,改变缓存区容量与跨运车数量进行实验。该实验算例中,跨运车数设置为1~9,缓存区容量设置为1~4,用以观察缓存区与跨运车对完工时间、岸桥平均使用率、跨运车平均使用率、岸桥等待时间的变化。实验中,岸桥与跨运车使用率计算如式(37)(38)所示: 每组实验取10 次有效值的平均值。实验结果如图6~9所示。 图6 完工时间比较Fig.6 Completion time comparison 如图6 所示,从横向上来看,在任务量相同的情况下,跨运车数的增加,可显著减少总完工时间。当跨运车数为1时,在四种缓存区的情况下,总完工时间都是最长的,而当跨运车的数增加到8 时总完工时间达到最小。当跨运车数超过6 后,缓存区容量大小不再影响总体完工时间。从纵向上来看,缓存区容量的增加可减少总体运行时间,当缓存区数量为3 时,再次增加缓存区容量,将无法影响完工时间。这是由于岸桥缓存区有足够的容量放置岸桥以及跨运车放置的集装箱,因此岸桥与跨运车可相对更加独立地进行装卸工作,减少了等待时间,因此完工时间减少。 如图7 所示,岸桥的平均使用率呈阶梯式增长。当缓存区容量为3、4 时,5 台跨运车即可达到局部最优; 图7 岸桥平均使用率比较Fig.7 Comparison of average utilization rate of quay crane 如图8 所示,跨运车的平均使用率呈增长趋势。与岸桥平均使用率(图7)不同的是,当跨运车数达到局部最优后,继续增加跨运车,跨运车使用效率会减小,这是由于跨运车设备过多而造成跨运车等待时间增加。因此对于决策者来说,安排大量的跨运车可降低作业时间成本,提高岸桥使用效率,但这种情况下会出现跨运车使用率降低的情况。 图8 跨运车使用率比较Fig.8 Comparison of average utilization rate of straddle carriers 从实验结果发现,缓存区与跨运车充足时,跨运车的使用效率在70%~85%,而岸桥的使用效率只有55%~65%,结合图9 所示,岸桥的等待时间稳定在400 s 左右,这是因为当出口箱数量大于进口箱数量时,总会有岸桥需要等待跨运车将出口箱运至缓存区。因此提高跨运车的性能或减少待装箱任务到岸桥缓存区的距离,双循环策略的优势将更加明显。从该实验中可以看到,缓存区的设置可以明显降低完工时间,提升岸桥与跨运车的使用效率,在该算例下,缓存区容量为3 即可满足系统最优。 图9 岸桥等待时间Fig.9 Waiting time of quay crane 实验2 岸桥与跨运车配比影响分析。 目前我国传统码头岸桥与集卡配比一般需要达到1∶5,而岸桥与集装箱跨运车配比一般只需要1∶3 即可完成相关任务(配比数据来源于振华重工)。传统码头一般为岸桥配置固定数量的集卡进行作业,而本文研究的是跨运车可以为任意一个岸桥服务,因此探究岸桥与跨运车总体系统配比具有重要意义。 实验2 中,设置岸桥数量为3,进行岸桥与跨运车配比研究。分别设置3 组实验,3 组实验的装箱量分别为15、30、45。缓存区容量设置为3,每组实验中岸桥与跨运车配比分别为1∶1(3-3),3∶4(3-4),3∶5(3-5),1∶2(3-6),3∶7(3-7),3∶8(3-8),1∶3(3-9)。“()”内为“(岸桥数-跨运车数)”。每组实验中集装箱量分别为15、30、45,用以观察在不同任务量的情况下,岸桥与跨运车配比对联合作业的影响。实验结果如图10~12 所示。 图10 完工时间变化情况Fig.10 Change of completion time 图11 岸桥使用率变化情况Fig.11 Changes in utilization rate of quay crane 通过实验结果可以看到,随着岸桥与跨运车配比增大,总完工时间逐渐减少。如图12 所示,岸桥与跨运车配比为3∶8 时,跨运车使用率出现峰值,此时再次增加跨运车,跨运车使用率减少,而完工时间没有明显变化。这是由于在缓存区的限制下,跨运车等待时间增长,造成拥堵情况。因此在双循环策略下,无需按照多个跨运车服务同一个岸桥进行操作,可根据岸桥数与任务量,安排岸桥与跨运车的总体系统配比,此时可以减少跨运车使用,减少码头设备量。 图12 跨运车使用率变化情况Fig.12 Changes in utilization rate of straddle carriers 本文引入双循环操作策略,研究了岸桥与跨运车的联合作业序列优化问题,以双循环岸桥和跨运车为研究对象,考虑了岸桥缓存区容量限制,岸桥双循环操作以及跨运车双循环运输策略,建立了以总完工时间最小化为目标的数学规划模型。针对禁忌搜索算法的局限性,设计了基于贪婪算法的响应性禁忌搜索算法进行求解并设计算例,验证了模型与算法的有效性。最后设计实验,对比岸桥缓存区容量和跨运车对完工时间、岸桥与跨运车使用率的影响,又研究了岸桥与跨运车数配比情况。最终得到算例实验下最优的跨运车数量、岸桥缓存区容量,以及合理的岸桥与跨运车配比。结果表明:缓存区的设置可明显减少完工时间、提高岸桥与跨运车使用率,双循环策略下设置合理的岸桥与跨运车联合作业序列,可减少跨运车的使用数量,减少码头设备。 本文在研究岸桥与跨运车的联合调度问题时,未考虑跨运车的翻箱问题,跨运车作为可自主在堆场与岸桥之间作业的运输设备,在堆场以及岸桥缓存区中可能存在翻箱问题,因此可以进一步考虑跨运车的翻箱问题。由于跨运车速率、堆场与码头前沿之间的距离对跨运车使用率以及总体作业时间影响较大,因此在大型码头,未来还可以考虑岸桥、跨运车以及其他运输设备的联合调度问题。
约束(28)(29)表示满足决策变量的限制。例如约束(28)表示,当j为出口箱,i为出口箱,i进入缓存区的时刻小于j进入缓存区的时刻,即Yki3.1 基本思想
3.2 基于贪婪算法的响应性禁忌搜索算法

若不是,则进入步骤12。
第四列表示跨运车编号,例如任务11 由编号为1 的跨运车进行操作,跨运车作业序列为,SC1:11-14-15-25,SC2:12-13-23,SC3:22-21-24。

否则进入步骤2.3)。
禁忌长度过长,可能造成搜索空间很小,搜索不充分。RTS算法通过在搜索过程中改变禁忌长度来避免此问题。RTS中禁忌长度T的选择基于解的重复次数与禁忌长度改变时间差。调整规则有两种方式:第一个方式是当解S两次连续重复出现之间的间隔regap在所设定的最大间隔gapmax之内,增加禁忌长度T=T×increase,扩大当前的搜索区域;
第二种方式是当前时间距离上次禁忌长度改变的时间超过预先设定的值,减少禁忌长度T=T×decrease,加强局部区域的搜索。当解S"的重复次数repeat,超过预先规定的解重复的最大次数remax,则将解S"加入禁忌表 。其中,increase为禁忌长度增加比例;
decrease为禁忌长度减少比例。
反之转步骤2.5)。
否则转步骤2.4)。
否则转步骤4。4.1 算例设计与求解结果

跨运车1 为14-15-11-12,跨运车2 为21-24-25-32,跨运车3 为23-22-31-33;
跨运车4 为35-13-34,具体调度安排如表7。


4.2 性能分析
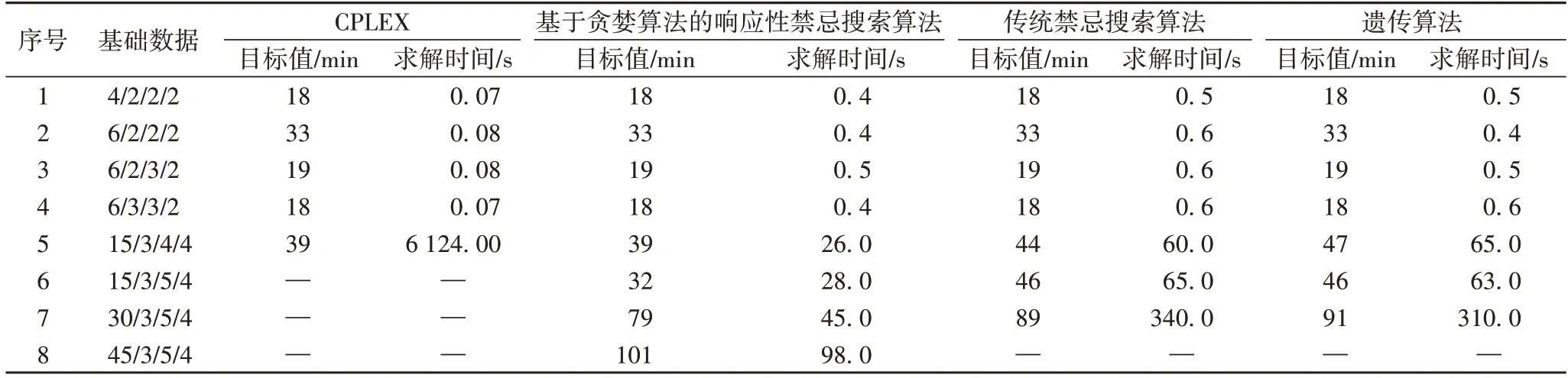
与遗传算法相比,本文算法在求解速度与求解效果方面都具有明显优势。4.3 参数配比实验研究及结论

而缓存区容量为1、2 时,需要7 台跨运车。因此合适的缓存区可以在保证岸桥使用率的情况下,减少跨运车的使用。