王 延,周 凯,沈守枫
(1.浙江工商大学 杭州商学院,浙江 杭州 311508;2.浙江工业大学 理学院,浙江 杭州 310023)
随着信息化建设的发展和信息技术的应用,高等学校积累了海量的数据,其中有结构化数据、半结构化数据和非结构化数据。数据科学的研究范围主要涉及且不限于数学、统计和计算机科学。对大数据的研究用到了现代基础理论知识(如线性代数、概率论、符号计算、数据库、分布式系统以及数据可视化等[1-2])。教务大数据的一个重要方面就是学评教大数据,即为保障课堂教学质量,学生可在每学期教学活动结束后对授课教师的教学模式进行定量化评价。学评教的本质是学生对学习课程的评价。如果教师在学期内主讲多门课程,教学管理部门可取多门课程平均成绩对教师进行评价。目前,学评教已经成为大部分高等院校保障课堂教学质量的重要方式。高校教学管理部门可依据学评教数据对课程与教师进行绩效考核,并作为学校支持一流课程建设与一流专业建设的标准。为全面评估课堂教学效果,教学管理部门往往会在学评教环节设计大量问题并收集相关数据。如何应用这些数据建立全面高效的评价体系,已经成为各高校管理部门研究的重点问题之一。
近年来,学者对教务大数据的研究主要集中在评价体系研究[3],而对于评价方法的研究较少,现有的研究并未讨论如何计算评教体系中不同指标的权重以及如何将权重综合为课程得分。为了使研究结果更加精准,并能很好地应用学评教所获得的数据,笔者基于某高校学评教大数据,从数学角度进行分析建模,运用熵权法、TOPSIS方法对课程进行定量化评价,并采用聚类分析、相关分析等数据挖掘方法对结果进行分析。
虽然高校间教学模式存在差异,教务大数据,特别是学评教大数据体系不尽相同,但皆可归结为如图1所示的5项指标,即兴趣引导、教学能力、教学资源、教学效果及教学内容。在每期末学评价考核时,学生可以针对这些指标对所学课程进行量化评分。

图1 高校教务大数据体系Fig.1 The evaluation system in university
兴趣引导用于衡量授课教师在授课过程中激发学生学习兴趣和引导学生学习自主性的能力。定义变量xi1用来表达第i门课程的授课教师在该指标上的得分。教学能力用于衡量授课教师对所授课程知识框架的掌握情况以及所展现的教学方式是否多样性。定义变量xi2用来表达第i门课程的授课教师在该指标上的得分。教学资源用于衡量授课教师在授课过程中是否提供丰富的资料,如教学课件、教学视频和试题库等资源。定义变量xi3用来表达第i门课程的授课教师在该指标上的得分。教学效果是从学生对知识的掌握度方面来评价授课教师的教学效果。定义变量xi4用来表达第i门课程的授课教师在该指标上的得分。教学内容衡量授课教师授课内容是否符合教学大纲以及教学计划。定义变量xi5用来表达第i门课程的授课教师在该指标上的得分。学评教指标的取分范围满足:xij∈{0,1,2,3,4,5},j=1,2,3,4,5。
由于5项指标具备不同的意义,故在评价过程中权重并不相同。采用熵权法[4]计算5项指标的权重信息。
首先,对学评教原始数据进行归一化处理,其计算式为
(1)

其次,计算每项指标的信息熵,其计算式为
(2)

(3)
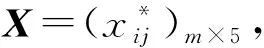
(4)
再次,结合熵权法所得的权重,计算每门课程与正负理想方案之间的加权距离,其计算式为
(5)
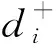
最后,计算每门被评价课程的得分,其计算式为
(6)
为了从学评教数据中挖掘信息反馈教学过程,采用相关分析与聚类分析对数据进行建模。基于式(6)得到的所有课程评价数据,采用K-means聚类方法对所有课程进行分类。K-means的数学模型描述为
(7)
式中:k为课程分类数,可以通过手肘法[6]确定聚类数量;Ci为第i类课程的类中心,即平均得分。
采用启发算法求解上述K-means聚类问题,步骤如下:
Step1随机选取k门课程作为初始聚类的类中心。
Step2将剩余m-k门课程按照与初始类中心的距离,以就近分配原则划分给上述k个类。
Step3基于新的聚类方案,计算形成的类别类中心,并将剩余课程划分给这k个类。
Step4判断是否满足聚类结束条件,如果不满足,转至Step 3。
Step5输出聚类方案以及类中心。
采用皮尔逊相关系数[7]分析课程评价得分的相关程度,其计算式为
(8)
式中:gi为第i门课程的学生平均绩点;r为课程评价得分与学生平均绩点间的相关系数。
同理,可以得到课程评估得分与各项指标间的相关性。定义第i门课程在第j项指标的得分为tij,其计算方式参照式(5,6),即
(9)
进而得到课程每项评价指标得分与学生课程绩点之间的相关系数,其计算式为
(10)
为验证笔者方法的可行性,笔者向高校教务部门收集某学期学评教大数据以及学生平均绩点大数据。
首先,对原始数据进行清洗,剔除异常数据并进行数据变换,进而得到3 707门课程在5项指标上的数据。运用式(2)得到各项指标的变异系数以及熵权系数,结果如表1所示。

表1 指标变异系数以及权重表Table 1 coefficient of variation and weight
然后,将表1中的权重数据代入式(5,6)可计算得到每门课程评价总分,对所有课程得分进行K-means聚类分析,将类数控制在2~10,得到对应的SSE(Sum of squares due to error)值,结果如图2所示。通过手肘法可发现k=2为最佳聚类数。

图2 课程得分聚类数与SSE间的关系Fig.2 The relationship of number of clusters and SSE
最后,将3 707门课程分成3类,其类中心的课程得分如图3所示。结果显示:第1类包含1 620门课程,平均得分44.110 1;第2类包含1 134门课程,平均得分30.389 6;第3类包含925门课程,平均得分58.337 3。
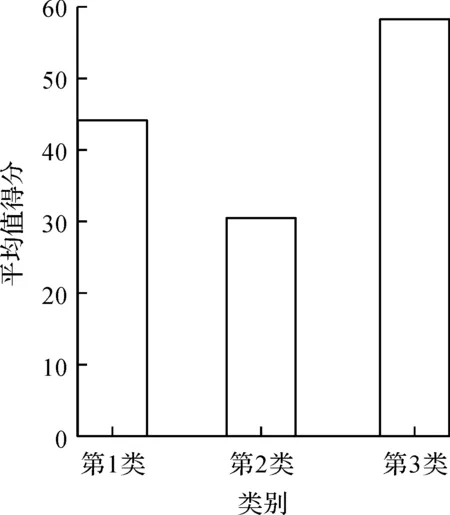
图3 3类课程平均得分Fig.3 The scores of the three classes
将3类课程类中心的5项指标平均得分数据分别用雷达图[8]展示,结果如图4~6所示。从图4~6中可以发现:3类课程在各指标上的得分较为接近,指标间差异并不明显。
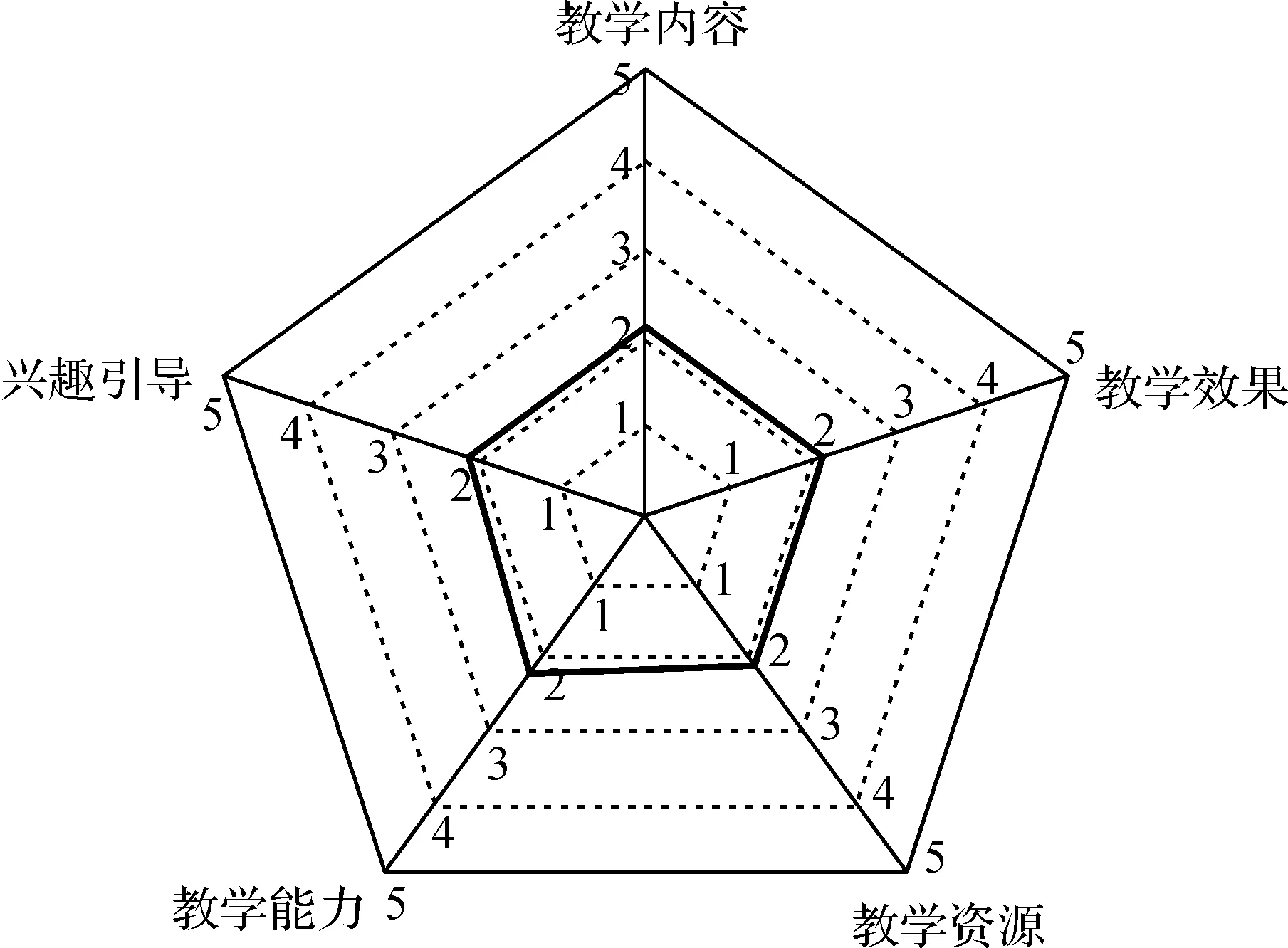
图4 第1类课程的指标雷达图Fig.4 The radar of the 1st class in different indexes
图5 第2类课程的指标雷达图Fig.5 The radar of the 2nd class in different indexes

图6 第3类课程的指标雷达图Fig.6 The radar of the 3rd class in different indexes
此外,笔者还进一步采集各门课程学生考核的平均绩点,运用相关分析理论研究学生绩点与教学指标之间的相关性,得到如下结果:学生平均绩点与
课程评价得分呈显著正相关,相关系数为0.516 7,显著性p<0.05。进一步分析学生平均绩点与课程评价指标之间的关系,得到相关系数分别为0.273 9,0.248 8,0.202 6,0.276 3,0.270 6。该结果表明:学生教学成绩与教师课堂兴趣引导、教学效果和教学内容呈现稍高的正相关性[9-12]。
基于高等学校海量的评教大数据,首先从兴趣引导、教学能力、教学内容、教学资源和教学效果等5项指标出发,采用熵权法定量计算各项指标的权重,建立了TOPSIS模型计算所有课程的评价得分;然后将所有课程按得分进行聚类分析,从而得到各类课程的教学特征;最后将课程考核平均绩点与各项指标得分进行相关分析,得出5项指标与课程成绩均呈现相关性,同时以泛函分析课程为例,应用多形式考核的研究生数学基础课学评教数据也得出了类似的结论。
本文得到了浙江工业大学校级研究生教改项目(2018126)的资助。
猜你喜欢绩点教务聚类教务排课对高等院校教学运行的作用分析大学(2021年2期)2021-06-11浅析高校教务管理存在的问题及对策传播力研究(2019年8期)2019-03-20基于完全学分制下的独立院校的平均绩点计算方法现代职业教育·高职高专(2018年10期)2018-05-14基于DBSACN聚类算法的XML文档聚类电子测试(2017年15期)2017-12-18基于高斯混合聚类的阵列干涉SAR三维成像雷达学报(2017年6期)2017-03-26浅谈新形势下高校教务管理人员的素质与培养信息记录材料(2016年4期)2016-03-11以培养方案为核心的教务管理系统开发的探索与实践当代教育理论与实践(2015年9期)2015-12-16一种层次初始的聚类个数自适应的聚类方法研究电子设计工程(2015年6期)2015-02-27自适应确定K-means算法的聚类数:以遥感图像聚类为例华东师范大学学报(自然科学版)(2014年6期)2014-02-27学分制下绩点设定形式探讨重庆科技学院学报(社会科学版)(2012年1期)2012-10-14