戚国庆 耿亚欣
(绍兴文理学院 土木工程学院,浙江 绍兴 312000)
边坡稳定性问题是边坡工程中一直在研究而且必须直面的问题,随着学科的不断深入发展,工程实践由粗放型向精细型转变,对边坡稳定性评估提出了更高的要求.传统的边坡稳定性分析方法如Fellenius法、Bishop法、Morgenstern-Price法[1-3]都是以边坡安全稳定性系数Fs=1为标准的确定性分析方法,没有考虑影响边坡稳定性的不确定性因素,而在岩土工程中确实存在很多的不确定性因素,因此安全系数法建立了许多简化的假定,故而得到的结果可能会存在偏差,以此来看,传统的确定性分析方法已经越来越难满足实际工程问题的需要.
不确定性包括物理不确定性、统计不确定性和模型不确定性,随机性是不确定性类型中的常见形式,其大小一般可以用概率来体现.可靠性分析[4]方法就是用概率表示边坡失稳的方法.其优点在于可靠性分析方法承认基本状态变量的随机性,将影响边坡稳定的因素作为随机变量考虑,将每一组的随机变量代入确定性边坡稳定分析方法[5],得到大量的确定性结果,运用统计学知识得出规律,用一个确定的概率值来描述边坡工程中的不确定性[6].从这方面来看,可靠性分析是边坡稳定性分析的更进一步发展,不确定性分析方法是确定性分析方法的延伸.
目前,较为常用的可靠性分析方法主要有5种,分别是蒙特卡洛法[7-8](Monte Carlo Method,MC),响应面法[9](Response Surface Method,RSM),可靠指标法[10],罗森布鲁斯统计矩法[11](Rosenblueth Method),随机有限元法(Stochastic Finite Element Method,SFEM),其中蒙特卡洛法[12-14]因其具有原理简单、精度高而且不需要分析参数概率分布、受问题条件限制的影响较小、结果是否收敛与极限状态方程的非线性无关等优点,经常作为检验其他分析方法的标准.本文以蒙特卡洛模拟方法为基准,用响应面法和罗森布鲁斯法与现行的边坡极限平衡法相结合,对边坡可靠性进行计算并对计算结果进行比较分析,探究更为合理的边坡稳定性预测方法.
1.1 蒙特卡洛法
边坡稳定性受到多种因素的影响,因此可以根据岩体结构、破坏机理和受力情况等建立边坡状态函数Z:
Z=g(X1,X2,…,Xm)
(1)

(2)
(3)
式中φ(1-Pf)指标准正态分布函数,可以根据得到的N个g(x)值求得均值μz和标准差σz:
(4)
(5)
也可根据均值μz和标准差σz可求得边坡可靠度指标β:
(6)
1.2 响应面法
边坡状态函数一般都是根据刚体极限平衡法Fs=R/S来建立.对于简单均质边坡,如果使用Fellinous法分析边坡稳定性,边坡状态函数尚可以用显式表达,但对略微复杂的边坡进行边坡稳定性分析,边坡状态函数通常无法用显式表达,此时可以通过用近似的边坡状态函数来替代真实的状态函数,此即响应面法.当得到近似边坡状态函数后,还需要结合其他的可靠度分析方法,常常与一次可靠度法相结合.

(7)
式中:A,Bi,Ci为待定系数,xi(i=1,2,3,…,n)为边坡随机变量.响应面极限状态方程求解步骤为:
1)假定初始点X0=(x1,x2,…,xn)通常会选择随机变量的均值点作为初始点.
3)解出由步骤(2)列出的线性方程组的解,得到待定系数A,Bi,Ci的值,于是得到以二次多项式表达的响应面极限状态方程.得到状态方程之后可以结合一次可靠度方法计算边坡可靠度和破坏概率,也可与蒙特卡洛法相结合.
1.3 罗森布鲁斯法
在状态变量Xi(i=1,2,3,…,n)分布函数未知的情况下,不必考察Xi的变化情况,只在区间(Xmin,Xmax)上分别对称地选择两个点,通常选取均值μXi的一个正负标准差σx,即:
(8)
若假设n个状态变量,则有2n个取值点,在2n个状态变量的组合下,由状态方程Z=G(x1,x2,…,xn)可求得2n个状态函数值Zj.若n个状态变量相互独立,则Z的均值为:
(9)
若n个状态变量相关,且2n个组合中每个组合出现的概率不相等,则变量间的相关系数ρ决定了每个组合概率值Pj:
+en-1enρn-1,n)
(10)
ρi-1,i为状态变量Xn-1与Xn之间的相关系数.式中ei(i=1,2,3,…,n)取值为:当xi取xi1时,ei=1;
当xi取xi2时,ei=-1.则Z的均值为:
(11)
如此便可推导出状态函数概率分布的一阶矩M1、二阶矩M2、三阶矩M3和四阶矩M4.
由边坡状态函数的一阶矩M1和二阶矩M2可求得边坡的可靠度指标β:
(12)
1.4 可靠度方法应用条件
可靠度分析方法有多种且计算方法有不同的使用条件,在实际计算使用过程中,为了获得较为准确的结果,要根据具体情况使用,故将以上常用几种可靠度方法的适用条件及优缺点进行分析,结果如下表1所示.

表1 可靠度方法应用条件综合分析表
2.1 计算模型
已知某简单均质土坡,分别在随机变量符合正态分布和对数正态分布情况下使用不同可靠度方法计算边坡可靠度.不考虑土性参数相关性,土体破坏符合摩尔库伦准则,该均质土坡高H=5.0 m,坡角β=45 °,土体容重γ=17.64 kN/m3,黏聚力c=6 kPa,内摩擦角φ=21 °,其几何尺寸如图1所示.

图1 均质边坡截面属性
使用有限元软件ABAQUS进行数值分析计算,运用强度折减法以数值计算不收敛作为依据,得到边坡稳定系数值Fs=1.16,图2、图3分别为ABAQUS分析得到的位移等值线云图和塑性应变等值线云图,由图可以清楚地判断边坡滑动面的位置,与极限平衡分析法得到的滑面大致相同,均呈大致的圆弧状,且都通过坡脚点.由安全系数值可以知道该边坡虽然达到了极限平衡,但依然属于欠稳定状态.在给定参数的情况下,利用定值使用不同极限平衡法计算得出边坡安全系数,如表2所示.

图2 位移等值线云图
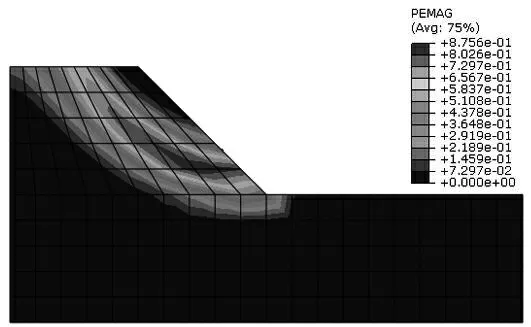
图3 塑性应变等值线云图

表2 不同极限平衡法的安全系数
2.2 参数变异性敏感度分析
针对该均质边坡,参考相关文献[16-17],假设随机变量c、φ相互独立,且变异系数范围为[0.1,0.3],因为主要考察不同可靠度方法之间的差异,因此忽略土的重度变异性对边坡可靠度的影响,土体参数统计结果如下表3所示.

表3 土性参数统计特征值
根据不同刚体极限平衡方法建立不同边坡状态函数,在土体参数符合正态分布情况下运用蒙特卡洛方法计算边坡可靠度,并以此作为基准.在同一变异系数下使用不同的可靠度方法计算,比较不同方法之间的差异;
在不同变异系数下计算可靠度,比较在同一可靠度方法下变异系数对可靠度的影响.
首先假设φ不变化,当c的变异系数在0.1到0.3之间变化时,分别在参数符合正态分布和对数正态分布下求得边坡的可靠度,结果如下图4(a)所示;
之后假设c不变化,φ的变异系数在0.1到0.3之间变化时,同样在参数符合不同分布下求得边坡可靠度,计算结果如下图4(b)所示,在参数符合不同分布下来考察参数变异性对边坡可靠度的影响.
2.3 参数分布类型敏感度分析
为了研究参数的分布类型对边坡可靠度的影响,依然选用三种(Fellenius法、Bishop法和Morgenstern-Price法)不同的极限平衡法建立边坡状态函数,在土体参数符合对数正态分布情况下计算边坡在不同变异系数下的可靠度,研究方法和上述正态分布情况下相同,计算结果如图5所示,将两种分布情况对比,探究参数在何种分布下对边坡可靠度影响更敏感.
2.4 结果分析
1)通过上述均质边坡算例,在相同变异系数下比较可以看出,使用不同刚体极限平衡法建立边坡状态函数时求得的可靠度指标有一定差异.使用Fellenius法求得的边坡可靠度最小,使用Bishop法求得的可靠度最大,M-P法求得的结果居中,但与Bishop法较为接近,这也与刚体极限平衡法求得的边坡安全系数相符合.边坡安全系数越大则可靠度越高,但同时也表明了边坡安全系数大于1时边坡仍然有破坏的可能.使用不同极限平衡法建立的状态函数计算的可靠度有差别是其固有缺陷,这是因为假定条件不同而导致的,Bishop法和M-P法的稳定系数是经过多次迭代求得,故而可靠性分析结果与蒙特卡洛法更为接近.
2)在不同变异系数下比较图4(a)、图5(a)可知,在φ不变的情况下,边坡可靠度随着c变异系数的增大而逐渐减小.从图4(b)、图5(b)可以看出在c不变的情况下,边坡可靠度也随着φ变异系数的增大而逐渐减小,可以知道边坡可靠度随着变异系数的增大而减小.进一步对比结果可以发现: 无论在何种分布下, 相同的边坡在φ变异系数变化时得到的可靠度指标更小,即边坡更易破坏,可以知道边坡可靠度指标对内摩擦角φ的变化更为敏感.
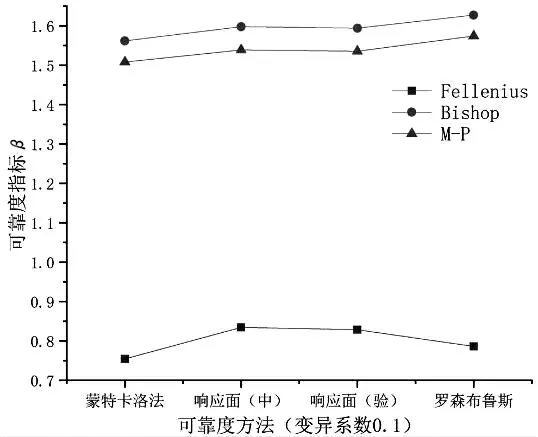
(a)c的变异系数0.1到0.3

(a)c的变异系数0.1到0.3
3)在不同参数分布类型但同一变异水平下研究发现:参数变异性较小时,两者计算的可靠度较为接近,但参数服从对数正态分布计算得到的可靠度数值偏大;
当变异系数较大时,对数正态分布下计算边坡可靠度比正态分布下计算偏差更大,可以知道参数在对数正态分布下,边坡可靠度对参数变异性更敏感.
1)运用可靠度方法对边坡进行可靠度分析时,能够充分考虑岩土参数的随机性、变异性等因素,能够量化各个参数对边坡稳定性的影响,解释了传统极限平衡法不能解释的安全系数大于1边坡破坏、安全系数小于1边坡稳定的问题.因此,将可靠度方法与边坡稳定性分析结合能更好地对边坡稳定性进行评价.
2)在相同的极限平衡法条件下建立边坡状态函数时,不同可靠度方法计算结果差异较小.对于一般边坡工程而言,罗森布鲁斯法和响应面法两者计算精度都能满足工程需要,如果工程对精度要求较高,应该通过响应面迭代或者选用高次响应面来拟合功能状态函数.
3)在不同的极限平衡法条件下建立边坡状态函数,可靠度计算结果差异较大,特别是在变异系数0.3时,Fellenius法具有更大的误差.在同一变异水平下,得到的可靠度指标最小的Fellenius法,其次是M-P法,最后是Bishop法.
4)从图可知,当土体参数在服从正态分布时能够取得较好的分析结果,在参数服从对数正态分布的情况下,计算结果误差明显增大,可知对数正态分布对可靠度影响更大.
5)c、φ变异性对边坡可靠度影响不同,无论何种分布,可以看出φ的变异性对边坡可靠度影响大于c的变异性对可靠度的影响.
猜你喜欢正态分布变异性安全系数碎石土库岸边坡稳定性及影响因素分析水利科技与经济(2022年12期)2022-12-26考虑材料性能分散性的航空发动机结构安全系数确定方法航空发动机(2021年1期)2021-05-22基于对数正态分布的出行时长可靠性计算重庆交通大学学报(自然科学版)(2017年3期)2017-05-17正态分布及其应用环球市场信息导报(2016年41期)2017-01-19电梯悬挂钢丝绳安全系数方法的计算中国质量监管(2016年1期)2016-12-13运动、健康与心率变异性的研究进展体育科研(2016年5期)2016-07-31χ2分布、t 分布、F 分布与正态分布间的关系湖北师范大学学报(自然科学版)(2015年3期)2015-12-05基于Copula函数对二维正态分布中常见认识误区的分析淮南师范学院学报(2015年3期)2015-03-22接近物体感测库显著提升安全系数汽车零部件(2014年6期)2014-09-20咳嗽变异性哮喘的中医治疗近况中医研究(2014年8期)2014-03-11