高云峰
(清华大学航天航空学院,北京 100084)
科学研究离不开系统与模型。系统是根据研究目的而人为界定,由一些有关联的物体或成份组成的有序整体。简单地说,系统就是我们关注或研究的对象,包含边界、成份和相互作用。模型是经过处理的简化系统,能体现原系统的本质特征,是描述和理解系统的有效工具。真实世界很复杂,但可以用简化的模型来描述。模型超越了我们可观察的范围,将不可见的、抽象的现象或特征形象化,有利于理解和研究。
模型可以直观反映系统的特征,特别是系统的内在特征,因此有时模型比实物更能展示出系统的特点,利用模型也更容易进行沟通和交流。模型与系统之间存在着某种相似性,除了可以解释一部分系统的现象,还可以通过模型预测系统更多的现象,甚至是还没有被发现的现象,从而在验证模型可靠性的同时,增加对系统的认识。例如,利用太阳系模型预测海王星的位置是模型预测的典型案例。
建立简化的模型来研究复杂的系统是一种科学研究的方法。模型包括物理模型(通常是实物或示意图)、数学模型(通常是数学公式)和概念模型(通常是相关理论)。
在目前的力学教学中,平时的习题或作业可以认为是已经简化好的模型,学生缺乏如何从真实系统简化为模型的训练(在本系列文章(2)中,从“工程问题”到“物理模型”,实际也是建模的过程)。
在教学过程中,笔者会把少量传统的习题进行改造,从实际问题或现象出发,给学生展示如何简化建模,如何分析得到结果并最终解释所关心的问题。这样的内容不用多,给学生开一个窗口,让学生了解一种重要的科学研究的方法和思路,而不仅仅是会做作业。
吉他、小提琴能演奏出优美的旋律,本质是琴弦振动的频率和幅度通过空气传到耳中(我们听到的旋律与振动频率相关,声音的强弱与振动幅度相关)。
以吉他为例,吉他由共鸣箱、琴颈、琴头及琴弦等部件组成,每根琴弦粗细不同,固定在琴桥与琴头之间,琴颈上有19根长品柱,第i个品柱与琴桥的距离为li(i=0,1,...,18) ,可以注意到这些距离从密到稀排列着(图1)。

图1 吉他照片
可以对琴弦振动进行建模,通过分析来解释与吉他相关的一些问题,包括上述现象。
首先将某根琴弦简化为无质量的弹簧,将琴弦质量简化为质点集中在弹簧中点,静止时琴弦已绷紧,设张力为T0。当质点有位移x时,单侧琴弦长度为d,张力为T(图2)。

图2 琴弦振动的简化模型
下面寻找系统参数之间的关系。单侧琴弦长度为

通常弹拨吉他时,琴弦的位移很小,因此设x是一阶小量。式(1)级数展开后保留一阶量,有

即琴弦振动时在忽略高阶小量的前提下长度不变。由于张力与琴弦伸长量有关,因此在振动过程中有

忽略重力(张力远大于琴弦重量),列写质点振动的动力学方程,有

由于位移x是小量,角度θ也是小量,有

将式(3)和式(5)代入式(4),有

设琴弦截面积为S,单位长度质量为ρ,则振动的固有频率为

下面利用式(7)来解释一些现象。
(1)琴头上有调紧琴弦的旋钮,有经验的吉他手演奏前要调整一下旋钮,通过改变琴弦的张力调整频率(图3)。式(7)表明频率ω与成正比,合理。

图3 琴头中的琴弦及旋钮
(2)琴弦有粗细之分(图3),粗弦用于演奏低音(低频),细弦用于演奏高音(高频)。式(7)表明频率与成反比,合理。相反如果6根琴弦一样粗细,高音对应的琴弦张力就明显增加,容易导致高音琴弦疲劳损坏。
(3)手按住琴弦某处,相当于琴头处的固定端移到手指处的品柱,改变了琴弦的长度,从而改变了振动频率。我们知道世界上把一组音(八度)分成十二个半音音程的律制,各相邻两音的振动频率之比完全相等,亦称“十二等程律”。式(7)表明频率与l成反比,因此图1中距离的比值也应该满足“十二等程律”,即前后距离之比为实际品柱与琴桥的距离见表1,相邻的距离比值见图4,合理。

表1 吉他各品柱的距离(根据实际照片测量)

图4 相邻品柱距离的比值
对音乐熟悉的读者可能会注意到,国际标准音的频率(表2)与表1中的部分品柱距离(黑体)竟然十分接近,我自己也感到有些不可思议(该吉他34寸(1寸 = 3.333 33 cm),全长866 mm,如果是其他品牌,品柱距离会变化,但比值不变)。

表2 C大调国际标准音频率
(4)实际吉他弹起来音色很丰富,而模型只有一个频率。原因是模型把质量集中为一个质点,这与实际不同。如果采用连续质量的模型,就更为接近实际的了。
大家可能注意到下雨时毛毛细雨与暴雨有一个明显区别:毛毛细雨是“飘”下来的(速度很小),而暴雨是“砸”下来的(速度很大)。如何用相关的力学知识,建立模型简要地解释这一现象呢?
建立坐标系,确定广义坐标y,分析运动和受力,画出受力图(图5)。

图5 雨滴受力分析
根据一般的经验,物体在空气中阻力为

其中CD为阻力系数(常数),S为物体横截面积,ρa为空气密度。
如果假设雨滴是球形,半径为r,水的密度为ρw,则有

根据图5,速度逐渐增加导致阻力增加,当满足阻力等于重力后,雨滴就一直以匀速运动(严格说是趋近于匀速运动)。由式(8)和式(9)获得雨滴的极限速度为

式(10)表明雨滴的速度与其半径有关,这就解释了暴雨速度大,毛毛雨速度小的现象。当然上述模型假设雨滴半径不变化,这不太合理,如果要更精细,可以修正模型。
考虑雨滴在下降过程中不断吸收周围的水汽,设周围大气相对地面静止,采用变质量模型[1],有

雨滴在单位时间内经过的空间是一个圆柱体,该圆柱内的水汽有部分被雨滴吸收(图6),设吸收率ζ为常数(ζ = 1表示全部吸收,ζ = 0表示不吸收;
吸收率ζ通常会很小,否则几滴雨就把运动路径上的水汽全吸收了),则

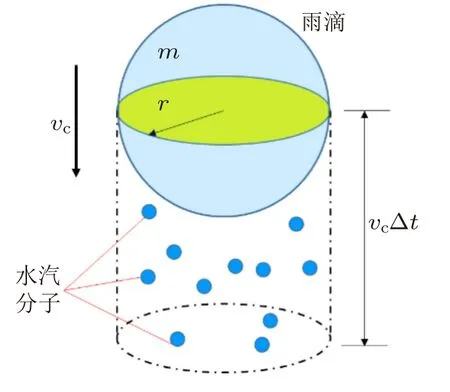
图6 考虑雨滴的变质量问题
将式(12)取极限后与式(11)联立,有
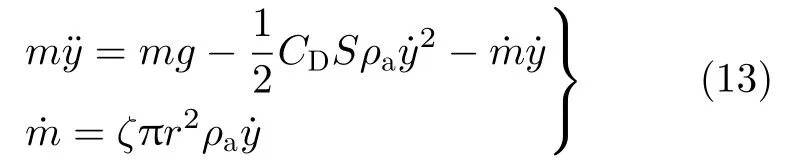
将式(9)改写,有

设y1=y,y2=y˙,y3=r,由式(13)和式(14)得到标准的一阶微分方程组,为

方程(15)耦合在一起,给出参数及初始条件 (ρw=1000kg/m3,ρa=1kg/m3,r(0)=0.02mm ,H=2000m ,CD=1 , 估 计 暴 雨 时ζ=0.005 ,中 雨 时ζ=0.001 , 小 雨时ζ=0.0006 ), 可 以 算出相关的数值解。
与前面雨滴质量和半径为常数的模型相比,变质量模型中雨滴不存在极限速度,而是随着高度减低,速度不断增加(图7)。雨滴变质量模型的计算结果与网上查到的数据很接近[2]:一般而言,毛毛雨的雨滴直径为0.5 mm, 而暴雨雨滴最大直径约为5.5 mm;
毛毛雨的收尾速度为2 m/s,而暴雨最大收尾速度为8~9 m/s(图8)。且同一高度落下的雨滴沿相同的“速度-直径”曲线变化,这一点还有待深入研究。
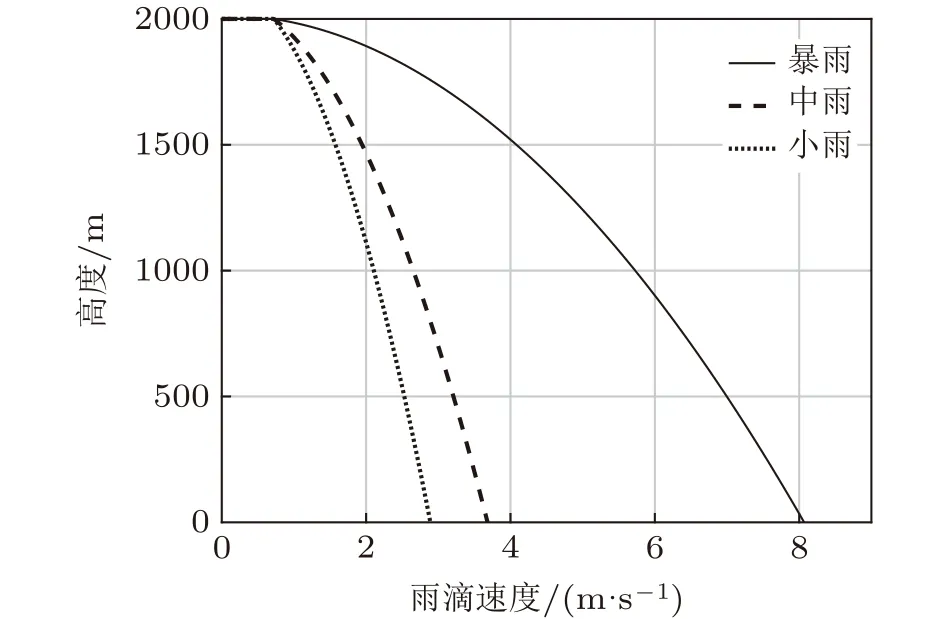
图7 雨滴高度与速度的关系

图8 雨滴直径与速度的关系
系统与模型是跨学科概念,可以应用在很多学科,力学模型主要研究系统的受力与运动的关系,可以迁移到其他领域:任何系统都可以建立类似“力与运动”的关系,只不过这里的“力”和“运动”更为广泛。例如在生物领域,“力”可以是生存压力,“运动”可以是种群数量的变化。
实际上,通过食物链关系,不同生物之间存在着某种制约关系(相当于分析力学中的约束),导致种群数目保持动态平衡。为了更好地理解这种制约及平衡关系,设想在一个理想的封闭草原环境中,存在野兔与野狼两种生物。很明显,野兔多则野狼食物充分,导致野狼数量增加;
而野狼数量太多,会通过捕食使野兔数量减少,反过来又导致部分野狼不容易找到食物而饿死,繁殖的数量也会下降。因此在这种生存竞争中,两种生物要么最终灭亡,要么经过一段时间后两者数量达到稳定的状态。
这一现象可以用Lotka-Volterra模型来描述,也称作猎食者-猎物(predator-prey)模型[3]。改写后,设野兔数量为R(rabbit),野狼的数量为W(wolf)。上述竞争关系可以表示为
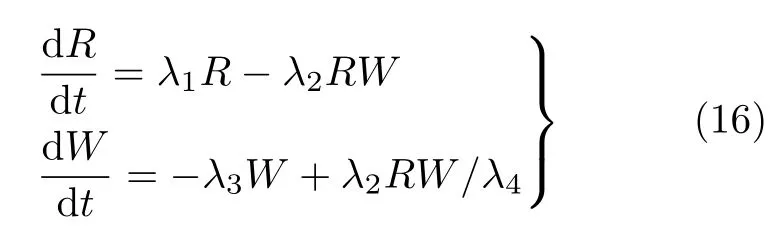
式中λ1是野兔的自然增长率(假定草场资源充沛),λ1R表示在单位时间出生的野兔;
λ2表示单位时间内野兔被野狼捕获的比例,λ2RW表示在单位时间被吃掉的野兔;
λ3是野狼的自然死亡率,λ3W表示在单位时间死亡的野狼;
λ4表示转换系数,表示平均吃λ4只野兔才生出1只小野狼。
给出适当参数和初始条件后,计算模拟发现野兔和野狼的数量的确呈现周期性的变化。其典型的情况是:从时间变化角度看,两者的数量振荡起伏(图9(a))。如果用水平轴和竖直轴分别表示它们的数量,会出现一个封闭的曲线(图9(b));
当然,如果参数不合适,会出现野狼把野兔全部吃完,(在封闭的环节下)野狼也会全部饿死的特殊“平衡”解。
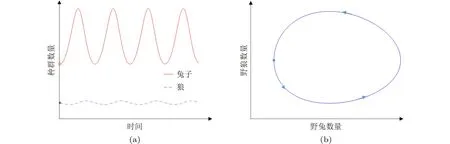
图9 野兔和野狼数量变化的关系
由此看出,在不同物种生存竞争这一问题中,不同物种的数目随时间在变化着,但是由于存在食物链关系,每个物种对另外的物种生存都会产生影响,从而导致最终达到一种“稳定”的状态,或动态的平衡。实际生物界有着复杂的食物链关系,模型更为复杂,但是大致仍有简单模型的特征:不同物种相互制约,长期趋于动态的平衡关系。
系统和模型是重要跨学科概念,可以应用于不同的学科领域。一般科研都要对系统进行简化,获得模型后,再进行深入研究。很多学生总感到理论与实际有巨大的鸿沟,最主要原因是缺乏建模的训练。有建模经验的学生可以将复杂问题(实际)简化后得到相对容易的模型(理论),然后就可以用不同的手段进行处理。
从以上案例中可以得出几点结论或启示。
(1)对琴弦的建模及分析并不复杂,得到的结果却可以解释很多相关现象,并且意外地发现某种吉他(34寸)的品柱距离与国际标准音的频率数值十分接近。因此简单的建模就可以解决很多问题,同时注意到模型是简化的系统,该模型解释不了实际琴弦音色丰富的问题。
(2)雨滴问题可以简单也可以复杂,均可以解释雨滴速度与尺寸的关系,这表明模型的复杂程度可以根据情况而定。注意到分析过程中有大量假设,如形状是球形、阻力与速度平方成比例、吸收率是常数等,这些可能与实际存在差距,也是模型的重要特点:模型是简化的系统,在简化时尽量有依据。对于变质量雨滴,计算中的参数参考了网上的数据,如云层高度、初始雨滴大小等,最终得到的雨滴速度和直径与网上资料十分接近。
(3)生物竞争的案例扩展了学生的视野,让学生了解建模的思想可以用于各个领域。同时有利于学生了解更广泛的约束概念,以及“力与运动”的关系。
如何根据系统的特点简化建模,是大学生应该掌握的重要能力。目前教学中给学生的往往是简化好的模型,学生缺少建模的训练。对学生来说,很多知识在考试后不久就可能忘了,而处理问题的方法和思维模式则可以一辈子不忘记。因此在教学中少量介绍一些建模的方法,让学生自行对一些有趣的现象进行简化分析,将使学生受益终身。
猜你喜欢野狼野兔琴弦野兔“教练”小猕猴智力画刊(2022年10期)2022-11-02小野狼饿了早期教育(家庭教育)(2021年10期)2021-12-17疯狂野兔,看招小哥白尼(野生动物)(2020年11期)2021-01-18小野兔的大耳朵小学阅读指南·低年级版(2020年12期)2020-12-04两只小野兔读友·少年文学(清雅版)(2020年11期)2020-03-29朱德庸漫画阅读(高年级)(2019年11期)2019-12-27当心大野狼创新作文(小学版)(2018年25期)2018-11-30野狼为什么总是嚎叫?儿童故事画报·智力大王(2017年10期)2018-03-14我把雨丝当做琴弦雨花(2015年12期)2016-01-18额头上的琴弦新作文·小学高年级版(2014年9期)2014-09-16