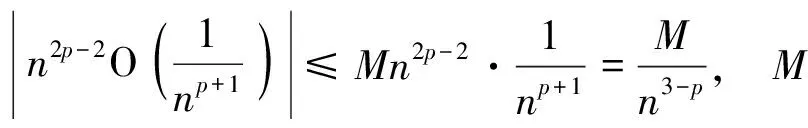黄永忠, 雷冬霞
(华中科技大学 数学与统计学院,武汉 430074)


然后考虑级数
得到它在p>2,p=2以及1 的相应结果(见命题2). 作为应用,计算级数 的和(见例1).p=2的情形就是2020年《美国数学月刊》的征解问题12215. 最后,在例2中利用rn(p)的等式讨论一类与p级数有关的极限. 引理1[3]对q∈(0,1),有 (1) 其中μ是与q有关的常数,且 (2) 注1 由引理1和等式 可得 (3) 引理2对p>1,有 (4) 从而由文献[2]的Euler-Maclaurin公式(式(19)),得 (5) 其中 注意到 令m→∞,由式(5)得 式(4)得证. 注2 由引理2和等式 可得 (6) 其中常数μ由式(2)得到(取q=p-1) 证因为 所以 (7) (i)若p=2,则由 得到 (ii)若p>2,则 (iii)若1 (8) 其中由q=p-1,依式(2),有 因此,结合上式和式(8),由式(7),得 令N→∞,得 事实上,对p>2和给定足够大的正整数n0,由引理2, 于是结合 得到 这里的M与p有关,但由式(5)和它随后的表达式知,M中不会出现分母为p-2的项,甚至M可以是一个关于p的线性式. 另一方面,对1 其中用到 其中 所以 其中 于是 (9) (i)若p=2,则由式(6),有 (也可由Stolz定理得到这个极限值),并由式(9)得 (ii)若p>2,则由式(6),有 并由式(9),得 (iii)若1 因此 从而由式(9),得 例1计算下列级数的和S: 解按照2020年《美国数学月刊》的征解问题12215的解答思路,有 于是由命题1和命题2,得 p级数的余项等式有助于处理与p级数有关的极限. 因为 所以 于是 (10) 再由引理2,得 (11) 因此 其中用到 (c)当1 其中用到 和 致谢作者非常感谢文献[2]和《美国数学月刊》的征解问题对本文的启发以及审稿专家提出的宝贵意见.