张路娟,郭良栋
(辽宁科技大学 理学院,辽宁 鞍山 114051)
在实际生活中,事物的变化趋势不仅取决于当前和未来的状态,也会取决于过去的状态,这种现象被称为“时滞”。时滞现象广泛存在于各种系统中,如生物系统[1]、神经网络系统[2]、经济系统[3]、网络控制系统[4]等。时滞的存在不仅影响系统的性能,甚至导致系统的不稳定。因此,时滞系统的稳定性分析以及控制问题成为控制工程领域中的一个热点问题。
对于单时变时滞系统,Lyapunov-Krasovskii(L-K)方法是常用的一种寻找系统时滞相关稳定性判据的方法。为了降低判据的保守性,学者们提出了众多不等式和方法,如Jensen不等式[5]、倒数凸不等式[6]、自由加权矩阵法[7]和时滞分解法[8]等。
在状态反馈网络控制中,由于物理设备、控制器、传感器和执行器位于不同的位置,会存在两种由网络引起的时间延迟,一种是从传感器到控制器,另一种是从控制器到执行器。闭环系统中出现的这两个时滞,由于信号传输条件的不同而具有不同的特性,故而把这两种时滞看作一种时滞是不合理的。基于远程控制和网络控制的应用背景下,Lam等[9]首次提出一种加性区间时滞系统的新模型,并获得时滞相关的稳定性判据。文献[10]利用两个连续相关的时滞分量构造新的LK泛函,并引入自由加权矩阵估计L-K泛函导数的上界,改进了文献[9]的模型。文献[11]结合倒数凸不等式对L-K泛函的导数进行严格估计,得到保守性较文献[10]更低的稳定性判据。
时滞分解法是一种有效降低稳定性判据保守性的方法,广泛应用于各种系统的稳定性分析中[12-13]。近年来,时滞分解法也被应用于两个加性时变时滞系统中。文献[14]将时滞分解法与扩展的倒数凸不等式相结合,得到一个改进的稳定性判据,但由于时滞区间被过多地划分,导致计算复杂度增加。文献[15]在文献[11]的基础上,利用时滞分解思想将系统中的时滞区间均匀地分成两个子区间,提出保守性更小的稳定性判据。文献[15]的计算复杂度低于文献[14],然而,当时滞子区间的长度相等时,并不总是可以得到时滞上界的最大值。
本文研究具有两个加性时变时滞系统的稳定性分析问题。考虑两个加性时变时滞分量的独立性和变化性,利用时滞不均匀分解的思想构造一类新的L-K泛函。结合对L-K泛函导数的严格估计,利用倒数凸不等式,以线性矩阵不等式(Linear matrix inequalities,LMIs)的形式给出新的时滞相关稳定性判据,通过一个数值算例验证本文的有效性和优越性。
Rn表示n维欧式空间,Rn×m是所有n×m维实矩阵的集合。一个实对称矩阵P>0(≥0)表示P是正定(半正定)矩阵。I表示具有适当维数的单位矩阵,如果没有明确说明,则假定具有兼容的维数。上标“T”表示矩阵的转置。
具有两个加性时变时滞的时滞系统

式中:x(t)∈Rn为系统的状态向量;
A,B∈Rn×n为常数矩阵;
φ(t)为初始条件;
d1(t)和d2(t)为具有不同特性的时滞变量。
时滞d1(t)和d2(t)满足条件

则系统(1)改写为

其中

本文的目的是建立系统(1)的时滞相关稳定性条件。以下引理将在推导过程中发挥重要作用。
引理1[5]设对任意常数矩阵M∈Rn×n,M=MT>0,存在标量α>0和向量函数ω,且ω:[0,α]→Rn,有不等式

引理2[6]设f1,f2,…,fN:Rm→R在Rm的开子集D上值非负,那么D上fi的倒数凸组合满足

使得

令ha=ah1,hb=bh2(0<a<1,0<b<1)。显 然0<ha<h1,0<hb<h2成立。将区间[0,h1]和[0,h2]分别划分为两个子区间,即[0,ha],[ha,h1]和[0,hb],[hb,h2]。针对C1~C4四种情况提出其相关稳定性判据。

为了简化矩阵表示,ei∈R9n×n(i=1,2,…,10)被定义为分块矩阵,例如
判据1满足式(3)和式(4)的系统(1)对于给定的标量0<a<1,0<b<1,h1,h2,μ1,μ,μ2>0,如果存在矩 阵当时滞满足C1时LMIs(7)和(11)成立,当时滞满足C2时LMIs(8)和(11)成立,当时滞满足C3时LMIs(9)和(11)成立,当时滞满足C4时LMIs(10)和(11)成立,则系统是渐近稳定的。

其中


证明对于C1:0≤d1(t)≤ha,0≤d2(t)≤hb,构造L-K泛函
其中
沿着系统(1)的轨迹对V(t)求导,则有


当0≤d1(t)≤ha,0≤d2(t)≤hb时,根据引理1和引理2,得到
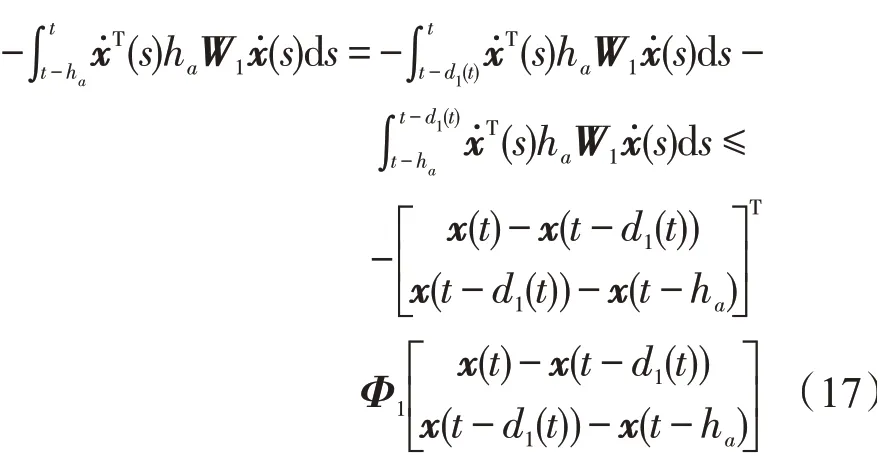
类似的


因此,得出结论
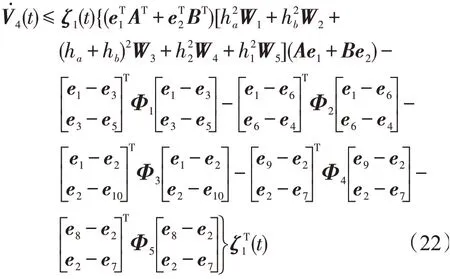
根据式(13)~式(22),得到

其中

对于C2:0≤d1(t)≤ha,hb≤d2(t)≤h2,构造L-K泛函

其中

同理可得
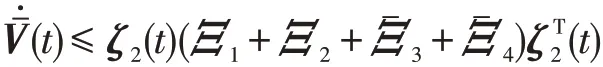
其中

对于C3:ha≤d1(t)≤h1,hb≤d2(t)≤h2,构造L-K泛函

其中

同理可得
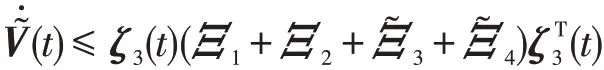
其中

对于C4:ha≤d1(t)≤h1,0≤d2(t)≤hb,构造L-K泛函
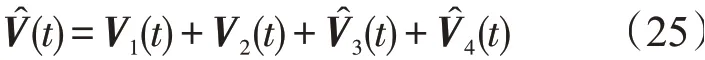
其中

V1(t),V2(t)见式(12)。
同理可得
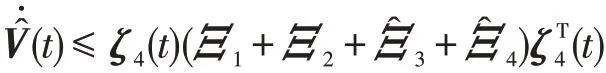
其中

因此,若LMIs(7)和(11)或(8)和(11)或(9)和(11)或(10)和(11)成立,有V̇(t)<0或Vˉ̇(t)<0或V͂̇(t)<0或V̂̇(t)<0。则当d1(t)和d2(t)分别满足C1或C2或C3或C4时,系统(1)是渐近稳定的。故判据1得证。
与文献[14-17]中使用的时滞分解法不同,本文利用动态时滞不均匀分解方法,将时滞区间[0,h1]和[0,h2]分别划分为[0,ha]、[ha,h1]和[0,hb]、[hb,h2]。子区间[0,ha]、[0,hb]的范围随着a和b的减小而减小,而子区间[ha,h1]、[hb,h2]的范围随着a和b的增加而减小。时滞间隔的范围越小,时变时滞d1(t)和d2(t)被获得的信息就越多。通过设置参数a和b的值可以获得更多的时变时滞信息,进而降低判据的保守性。注意到,当a=1/2,b=1/2时,本文划分的四个不均匀时滞子区间退化为文献[15]的时滞子区间。因此,本文所得的系统稳定性判据较文献[15]更具一般性。
表1为给定时滞上界h1时所获得的时滞上界h2,表2为给定时滞上界h2时所获得的时滞上界h2。当h1=1或1.2或1.5时,利用判据1所得时滞上界h2显著大于文献[14-17]时滞上界,表明本文稳定性判据具有更低的保守性。

表1 给定d1(t)的上界h1计算时滞d2(t)的上界h2Tab.1 Calculated upper bound h2 of time delay d2(t)at given upper bound h1 of d1(t)

表2 给定d2(t)的上界h2计算时滞d1(t)的上界h1Tab.2 Calculated upper bound h1 of time delay d1(t)at given upper bound h2 of d2(t)
表3给出本文判据与相关文献决策变量的数量。与现有文献相比,本文判据具有较少的决策变量,较低的计算复杂度。

表3 各方法决策变量数Tab.3 Decision variables of each method
讨论了具有两个加性时变时滞系统的稳定性问题。利用动态时滞不均匀分解、积分不等式等方法,得到系统的稳定性判据。判据的优点在于具有更小的保守性和更低的计算复杂度。最后给出数值算例,进一步说明判据的优越性和可行性。
猜你喜欢时变时滞复杂度随机时滞微分方程的数值算法实现烟台大学学报(自然科学与工程版)(2021年1期)2021-03-19毫米波MIMO系统中一种低复杂度的混合波束成形算法成都信息工程大学学报(2021年6期)2021-02-12变时滞间隙非线性机翼颤振主动控制方法北京航空航天大学学报(2020年10期)2020-11-14Kerr-AdS黑洞的复杂度华东师范大学学报(自然科学版)(2020年1期)2020-03-16|直接引语和间接引语|阅读与作文(英语初中版)(2019年11期)2019-09-10非线性电动力学黑洞的复杂度华东师范大学学报(自然科学版)(2019年2期)2019-06-11不确定时滞奇异摄动系统的最优故障估计北方工业大学学报(2019年5期)2019-03-30中立型随机时滞微分方程的离散反馈镇定上海师范大学学报·自然科学版(2018年3期)2018-05-14基于马尔可夫时变模型的流量数据挖掘软件(2017年9期)2018-03-02基于时变Copula的股票市场相关性分析智富时代(2017年4期)2017-04-27